Jupyter Snippet CB2nd 07_rolling_average

4.7. Implementing an efficient rolling average algorithm with stride tricks

import numpy as np
from numpy.lib.stride_tricks import as_strided

def aid(x):
    # This function returns the memory
    # block address of an array.
    return x.__array_interface__['data'][0]

n = 5
k = 2
a = np.linspace(1, n, n)
ax = aid(a)

as_strided(a, (k, n), (8, 8))

array([[ 1e+000,  2e+000,  3e+000,  4e+000,  5e+000],
       [ 2e+000,  3e+000,  4e+000,  5e+000,  9e-321]])

def shift1(x, k):
    return np.vstack([x[i:n - k + i + 1]
                      for i in range(k)])

def shift2(x, k):
    return as_strided(x, (k, n - k + 1),
                      (x.itemsize, x.itemsize))

b = shift1(a, k)

b

array([[ 1.,  2.,  3.,  4.],
       [ 2.,  3.,  4.,  5.]])

aid(b) == ax

False

c = shift2(a, k)

c

array([[ 1.,  2.,  3.,  4.],
       [ 2.,  3.,  4.,  5.]])

aid(c) == ax

True

n, k = 1000, 10
t = np.linspace(0., 1., n)
x = t + .1 * np.random.randn(n)

y = shift2(x, k)
x_avg = y.mean(axis=0)

import matplotlib.pyplot as plt
%matplotlib inline

fig, ax = plt.subplots(1, 1, figsize=(8, 4))
ax.plot(x[:-k + 1], '-k', lw=1, alpha=.5)
ax.plot(x_avg, '-k', lw=2)

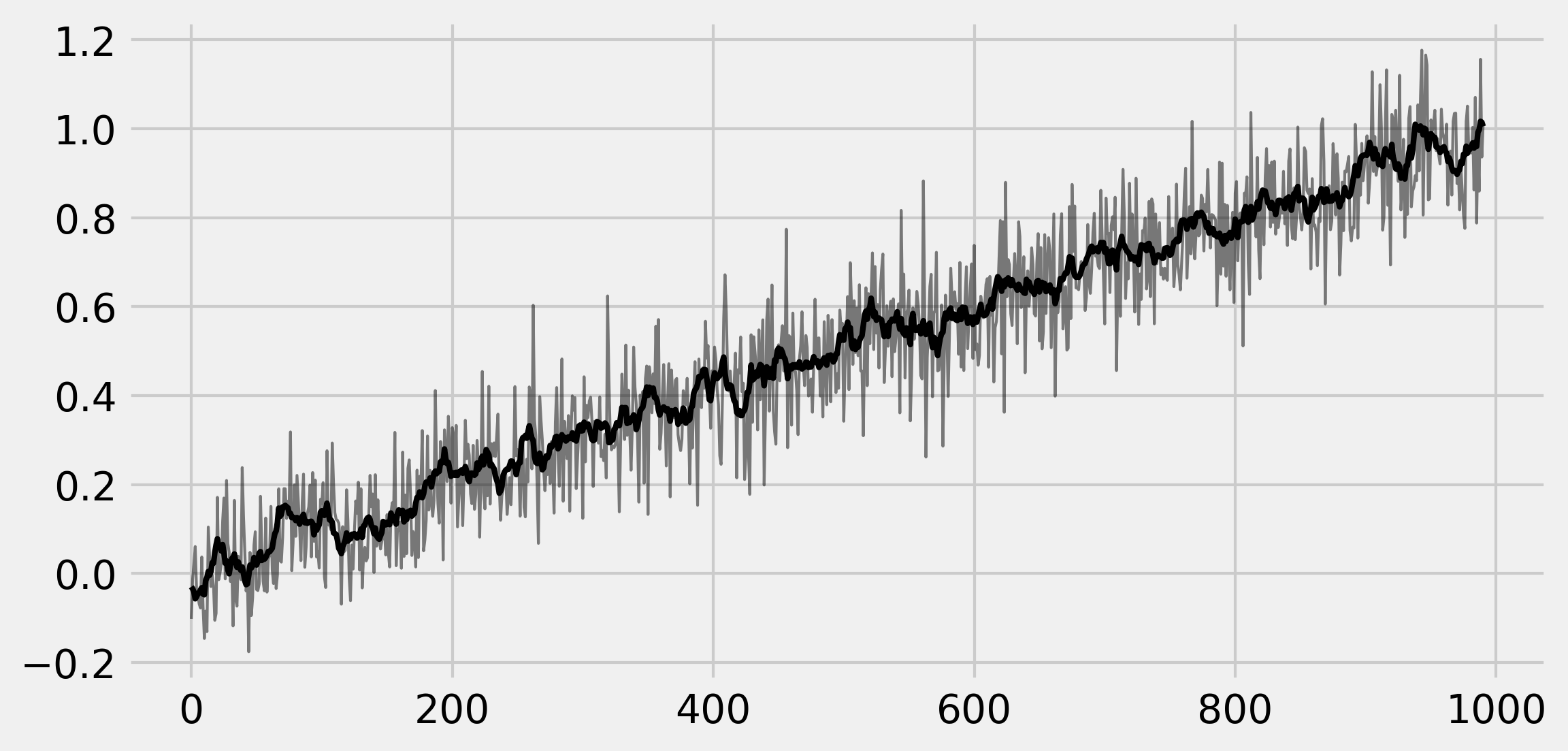
%timeit shift1(x, k)

15.4 µs ± 302 ns per loop (mean ± std. dev. of 7 runs,
    100000 loops each)

%%timeit y = shift1(x, k)
z = y.mean(axis=0)

10.3 µs ± 123 ns per loop (mean ± std. dev. of 7 runs,
    100000 loops each)

%timeit shift2(x, k)

4.77 µs ± 70.3 ns per loop (mean ± std. dev. of 7 runs,
    100000 loops each)

%%timeit y = shift2(x, k)
z = y.mean(axis=0)

9 µs ± 179 ns per loop (mean ± std. dev. of 7 runs,
    100000 loops each)